Sucesiones
Desde tiempos inmemoriales la humanidad ha tratado de predecir sucesos y acontecimientos.
Si tenemos varios objetos que están ordenados mediante una ley que no conocemos explícitamente, sentimos curiosidad o necesidad por poder predecir el término siguiente.
Con el nombre de sucesiones o progresiones se les llama a las funciones cuyos valores, las imágenes, los podemos numerar y ordenar en forma correlativa, cómo los números naturales. Esto es, podemos hablar de un primer elemento o término inicial, un segundo, uno tercero, y así sucesivamente, siempre que haya una relación que se cumple en forma estricta, siempre, aunque no la conozcamos.
Por ejemplo, si hablamos de los nombres de los alumnos de una clase, ordenados en forma alfabética, tenemos una sucesión: Andrés, Beatriz, Carlos, Carolina, Daniel, .........
En una manada de ciervos se puede predecir la población a lo largo del tiempo, siendo esta una función, entre otras variables, de la cantidad de pasto, que a su vez depende del número de insectos. La población inicial es el primer término, luego el segundo es la población al otro año, y así seguimos.
Un ejemplo de sucesión sería este
X1 = 1
X2 = 3
X3 = 5
.....
siendo el término n-ésimo:
Xn = 2·n - 1
Esta sucesión representa a los números impares. A simple vista se puede ver que desde el punto de vista de la notación, la sucesión presenta una enorme ventaja. Permite expresar infinitos números en una expresión muy corta. En el caso del ejemplo anterior:
f(n) = 2·n - 1
Si sustituimos el término n por cualquier valor natural obtenemos automáticamente el término correspondiente de la sucesión. Como sucede con otras herramientas, como las matrices, la sucesión permite abreviar notablemente las expresiones y ahorrar en cálculos.
Las aplicaciones de las sucesiones son incontables. Se utilizan abundantemente para demostrar los teoremas y las propiedades de la topología matemática, y en la muy conocida demostración del número pi, pero dado que esta parte del cálculo es la más inocua, son mucho más destacadas sus aplicaciones en materia de cálculo numérico.
Las series numéricas son la suma de los términos de una sucesión y la materia más densa de la primera parte de la asignatura cálculo del primer curso de cualquier carrera técnica. Existen varios tipos de series en función de la naturaleza de la sucesión que las conforma, que pueden ser aritméticas, geométricas, basadas en funciones trigonométricas, logarítmicas, exponenciales, etcétera... Pues calcular la suma de términos de las sucesiones es de aplicación para calcular el error máximo que obtenemos al realizar una operación por un método de cálculo numérico iterativo.
A los términos de una sucesión se los denomina según el lugar que ocupan. Al primer término lo llamamos a1, al segundo a2, al tercero a3, y así en general, al término que ocupa el lugar n lo llamamos an.
Definición: Las sucesiones son funciones de dominio natural.
Por comodidad se acostumbra a empezar en el uno. Entonces el dominio son los números naturales menos el cero.
El dominio es el conjunto de los números naturales positivos y el codominio es el conjunto de los números reales. Por ejemplo los primeros términos de la sucesión f(n) son:
fn | ||
f1 | 2 | 2 |
f2 | 2+3 | 5 |
f3 | 5+3 | 8 |
f4 | 8+3 | 11 |
f5 | 11+3 | 14 |
En el ejemplo anterior se trata de una sucesión aritmética porque cada término difiere del anterior en una cantidad constante llamada diferencia. En este caso, esa constante vale 3.
¿Podremos llegar a una fórmula general de cualquier término? ¿Podremos calcular el término que ocupa el lugar número 101 sin tener que hacerlos todos?
Vamos a escribir de nuevo los términos, pero sin hacer ninguna operación:
fn | ||
f1 | 2 | 2 |
f2 | 2+3 | 5 |
f3 | 2+3+3 | 8 |
f4 | 2+3+3+3 | 11 |
f5 | 2+3+3+3+3 | 14 |
El quinto término, esto es, el 14, ¿cuántas veces tiene incluido el número 3? Respuesta: 4 veces, porque la primera vez no le sumamos nada, y en las demás veces le sumamos el 3.
Entonces, el quinto término es 2 + 4 veces el número que se repite, el 3.
Entonces, el sexto término será 2 + 5 veces el número que se repite, el 3.
Entonces, el término número 101 es 2 + 100 veces el número que se repite, el 3.
Esto es, 2 + 3 x 100= 302.
En general, el término que ocupa el lugar n será an=2 + 3 x (n-1)
| a1 | al primer término |
| an | al último término |
| d | la diferencia constante |
| n | número de términos |
TIPOS DE SUCESIONES
Las sucesiones convergentes son las sucesiones que tienen límite finito.
Límite = 0
Límite = 1
Sucesiones divergentes
Las sucesiones divergentes son las sucesiones que no tienen límite finito.
Límite = ∞
Sucesiones oscilantes
Las sucesiones oscilantes no son convergentes ni divergentes. Sus términos alternan de mayor a menor o viceversa.
1, 0, 3, 0, 5, 0, 7, ...
Sucesiones alternadas
Las sucesiones alternadas son aquellas que alternan los signos de sus términos. Pueden ser:
Convergentes
1, −1, 0.5, −0.5, 0.25, −0.25, 0.125, −0.125,..
Tanto los términos pares como los impares tienen de límite 0.
Divergentes
1, 1, 2, 4, 3, 9, 4, 16, 5, 25, ...
Tantos los términos pares como los impares tienen de límite +∞.
Oscilantes
−1, 2, −3, 4 ,−5, ..., (−1)n n
Sucesiones monótonas

Sucesiones estrictamente crecientes
Se dice que una sucesión es estrictamente creciente si cada término es mayor que el anterior.
an+1 > an
2, 5, 8, 11, 14, 17,...
5 > 2; 8 > 5; 11 > 8; ...
Sucesiones crecientes
Se dice que una sucesión es creciente si cada término es mayor o igual que el anterior.
an+1 ≥ an
2, 2 , 4, 4, 8, 8,...
2 ≥ 2; 4 ≥ 2; 4 ≥ 4; ...
Sucesiones estrictamente decrecientes
Se dice que una sucesión es estrictamente decreciente si cada término de la sucesión es menor que el anterior.
an+1 < an
1, 1/2, 1/3, 1/4, 1/5, 1/6,...
1/2 < 1; 1/3 < 1/2 ; 1/4 < 1/3; ...
Sucesiones decrecientes
Se dice que una sucesión es decreciente si cada término de la sucesión es menor o igual que el anterior.
an+1 ≤ an
Sucesiones constantes
Se dice que una sucesión es constante si todos su términos son iguales, an= k.
an = an+1
5, 5, 5, 5, ...
Sucesiones acotadas inferiormente
Una sucesión está acotada inferiormente si todos sus términos son mayores o iguales que un cierto número K, que llamaremos cota inferior de la sucesión.
an ≥ k
A la mayor de las cotas inferiores se le llama extremo inferior o ínfimo.
Si el ínfimo de una sucesión es uno de sus términos se le llama mínimo.
Toda sucesión acotada inferiormente es creciente.
Sucesiones acotadas superiormente
Una sucesión está acotada superiormente si todos sus términos son menores o iguales que un cierto número K', que llamaremos cota superior de la sucesión.
an ≤ k'
A la menor de las cotas superiores se le llama extremo superior o supremo.
Si el supremo de una sucesión es uno de sus términos se llama máximo.
Toda sucesión acotada superiormente es monótona decreciente.
Sucesiones acotadas
Una sucesión se dice acotada si está acotada superior e inferiormente. Es decir si hay un número k menor o igual que todos los términos de la sucesión y otro K' mayor o igual que todos los términos de la sucesión. Por lo que todos los términos de la sucesión están comprendidos entre k y K'.
k ≤ an ≤ K'
Conociendo el primer término a1 y la diferencia de una progresión aritmética se calcula el término general de la sucesión por la siguiente fórmula:

Término general de una progresión aritmética
El término general de una progresión aritmética es aquel en el que se obtiene cualquier término sumándole la diferencia al término anterior. El término de una progresión aritmética es la expresión que nos da cualquiera de sus términos, conocidos alguno de ellos y la diferencia de la progresión. La fórmula del término general de una progresión aritmética es:Donde d es un número real llamado diferencia. Si el término inicial de una progresión aritmética es
 y la diferencia común es
y la diferencia común es  , entonces el término
, entonces el término  -ésimo de la sucesión viene dada por
-ésimo de la sucesión viene dada por , n = 0, 1, 2,... si el término inicial se toma como el cero.
, n = 0, 1, 2,... si el término inicial se toma como el cero. n = 1, 2, 3,... si el término inicial se toma como el primero.
n = 1, 2, 3,... si el término inicial se toma como el primero.
tenemos quede diferencia
sumando miembro a miembro todas esas igualdades, y simplificando términos semejantes, obtenemos:
- ...
(I)expresión del término general de la progresión, conocidos su primer término y la diferencia. Pero también podemos escribir el término general de otra forma. Para ello consideremos los términos
 y
y  (
( ) de la progresión anterior y pongámolos en función de
) de la progresión anterior y pongámolos en función de  :
:Restando ambas igualdades, y trasponiendo, obtenemos:
(II)expresión más general que (I) pues nos da los términos de la progresión conociendo uno cualquiera de ellos, y la diferencia.
Dependiendo de que la diferencia
 de una progresión aritmética sea positiva, nula o negativa, tendremos:
de una progresión aritmética sea positiva, nula o negativa, tendremos:- d>0: progresión creciente. Cada término es mayor que el anterior.
- d=0: progresión constante. Todos los términos son iguales.
- d<0: progresión decreciente. Cada término es menor que el anterior.
-Progresiones Geométricas
Las Progresiones Geométricas son sucesiones en las que cada término se obtiene multiplicando por una misma cantidad r -que puede ser positiva o negativa- al término anterior. Es decir: an=an-1.r. La cantidad r por la que se va multiplicando se llama razón. Las sucesiones cn y en de los ejercicios anteriores son progresiones geométricas de razón d=0'5 y d=10 respectivamente.
Conociendo el primer término s1 y la razón de una progresión geométrica se calcula el término general de la sucesión por la siguiente fórmula:
También es posible hallar la suma de los n primeros términos de una progresión geométrica. Para ello utilizamos la fórmula:

- La progresión 1, 2 ,4 ,8 ,16, es una progresión geométrica cuya razón vale 2, al igual que 5, 10, 20, 40.
- La razón no necesariamente tiene que ser un número entero. Así, 12, 3, 0.75, 0.1875 es una progresión geométrica con razón 1/4.
- La razón tampoco tiene porqué ser positiva. De este modo la progresión 3, -6, 12, -24 tiene razón -2. Este tipo de progresiones es un ejemplo de progresión alternante porque los signos alternan entre positivo y negativo.
- Cuando la razón es igual a 1 se obtiene una progresión constante: 7, 7, 7, 7
- Un caso especial es cuando la razón es igual a cero, por ejemplo: 4, 0, 0, 0. Existen ciertas referencias que no consideran este caso como progresión y piden explícitamente que
 en la definición.
en la definición.
Fuente:
http://es.wikipedia.org/wiki/Progresi%C3%B3n_aritm%C3%A9ticaWikipedia
http://www.edu.mec.gub.uy/banco%20de%20recursos/matematica/sucesiones.htm
http://www.vitutor.com/al/sucesiones/suc2_Contenidos.html
http://es.wikipedia.org/wiki/Progresi%C3%B3n_geom%C3%A9trica
http://anjaander.blogspot.com/2008/01/sucesiones-matemticas.html



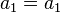
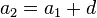





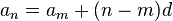
1 comentario:
Coloca los nombre de los autores o la dirección de donde lo sacaste
Publicar un comentario