Introducción:
Conjunto de los números reales
Está formado por el conjunto de los números enteros, racionales e irracionales, en adelante lo vamos a denotar por R; gráficamente el conjunto de los números reales lo podemos representar por una recta en la que fijamos un origen y una unidad, que hace que a cada punto de la recta le corresponda un número real y a cada número real le corresponda un punto de la recta. A esta recta la denominamos la recta real

Función:
Es una relación entre los elementos de dos conjuntos, de forma que a determinados elementos del primer conjunto se asocian elementos del segundo conjunto de manera unívoca, es decir que a un elemento del primer conjunto no le podemos asociar más de un elemento del segundo conjunto. A un elemento cualquiera del primer conjunto lo representamos con la letra x, que denominamos variable independiente y al único elemento que le corresponde en el segundo conjunto lo representamos por la letra y, a la que denominamos variable dependiente. A la relación la representamos por la letra f y escribimos y=f(x).
Dominio de definición de una función f :
Es el conjunto de valores de x para los que la función f(x) existe. Lo representamos por Dom(f).
Recorrido o imagen de una función f :
Es el conjunto de valores que toma la variable dependiente y. Lo representamos por Img(f).
Función real de variable real :
Es aquella cuyo dominio y recorrido son subconjuntos del conjunto de los números reales.
Las funciones reales de variable real se suelen representar en el plano, utilizando un sistema de referencia. En la figura que sigue, la primera gráfica, es la gráfica de una función ; la segunda, no es la gráfica de una función:

En el primer caso a cada valor de x le corresponde un único valor de y. En el segundo caso, hay valores de x que no están únicamente determinados.
Una función puede definirse mediante una expresión verbal, una tabla, una fórmula o una gráfica. En general trabajaremos con funciones expresadas mediante una fórmula o expresión analítica y su gráfica. Según la expresión analítica clasificamos las funciones de la siguiente forma:

Intervalos y entornos
Definimos sobre la recta real :

El conjunto [a,b] se llama intervalo cerrado y (a,b) se llama intervalo abierto. En cualquiera de los casos b-a se llama longitud del intervalo.
Entorno de un número real x:

Límite de una función en un punto

Los valores de x a considerar han de pertenecer al dominio de definición , D de la función. También es necesario que en D haya puntos tan próximos a a como queramos, es decir, que a sea un punto de acumulación de D.
Explicación dinámica del concepto de punto de acumulación
Puntos tan próximos como queramos significa que cualquiera que sea la distancia que consideremos, por muy pequeña que sea, existen puntos del dominio de definición de la función, que no coincidan con "a", a una distancia de "a" menor que la considerada.
Ejemplo dinámico de un punto "a" que no es punto de acumulación
El límite depende únicamente del comportamiento de la función en las proximidades de a, no de cual sea el valor de la función en el punto a ; de hecho, a puede no pertenecer al dominio de definición de la función. Sí es necesario, que "a" sea punto de acumulación del dominio de definición de la función.
Explicación dinámica del concepto de límite
Ejemplo : Una función típica en análisis es :

Esta función no está definida en el punto x=1 . Para este valor de x, el denominador de la función es 0 , y no tiene sentido en matemáticas dividir por 0. El valor al que esta función se aproxima, cuando x tiende a 1 por la izquierda o por la derecha, es 2. Luego la función tiene límite cuando x se aproxima a 1 ; el límite es 2.
Escribimos:

Límites laterales:
El límite lateral por la izquierda de una función y=f(x) en el punto x = a es el valor al que se aproxima f(x) cuando x se aproxima al valor de a por valores menores que a . Lo representamos por :
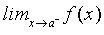
El límte lateral por la derecha de una función y = f(x) en el punto x = a es el valor al que se aproxima f(x) cuando x se aproxima al valor de a por valores mayores que a . Lo representamos por :

Ejemplo:

Límite de una función en el infinito

Ejemplo:



No hay comentarios:
Publicar un comentario