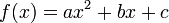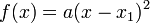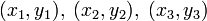Ejercicios Progresion Geometrica y Aritmetica - Ferreyra William

Ejercicios de progresion geométrica
El 2º término de una progresión geométrica es 6, y el 5º es 48. Escribir la progesión.


1er termino = (2)
2do termino = (6)  =  2x3    
3er termino = (12) =  2x6 
4to termino = (24) =  2x12
5to termino = (48) =  2x24

2,6,12,24,48,




Ejercicios de progresion aritmética
El cuarto término de una progresión aritmética es 10, y el octavo es 20. Escribir la progesión.

1er termino = 2.5
2do termino = 5   = (2.5+2.5)
3er termino = 7.5 = (2.5+5)
4to termino = 10  = (2.5+7.5)
5to termino = 12.5 = (2.5+10)
6to termino = 15  =  (2.5+12.5)
7mo termino = 17.5 = (2.5+15) 
8vo termino = 20  =  (2.5+17.5)

2.5,5,7.5,10,12.5,15,17.5,20,

Listo creo q estan bien

Ejercicio de Funcion Cuadratica

Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.

f(x) = ax² + bx +c

Representación gráfica de la parábola

Podemos construir una parábola a partir de estos puntos:

1. Vértice

Por el vértice pasa el eje de simetría de la parábola.

La ecuación del eje de simetría es:

2. Puntos de corte con el eje OX

En el eje de abscisas la segunda coordenada es cero, por lo que tendremos:

ax² + bx +c = 0

Resolviendo la ecuación podemos obtener:

Dos puntos de corte: (x₁, 0) y (x₂, 0) si b² − 4ac > 0

Un punto de corte: (x₁, 0) si b² − 4ac = 0

Ningún punto de corte si b² − 4ac < 0

3. Punto de corte con el eje OY

En el eje de ordenadas la primera coordenada es cero, por lo que tendremos:

f(0) = a · 0² + b · 0 + c = c        (0,c)

Representar la función f(x) = x² − 4x + 3.

1. Vértice

x _v = − (−4) / 2 = 2     y _v = 2² − 4· 2 + 3 = −1       

 V(2, −1)

2. Puntos de corte con el eje OX

x² − 4x + 3 = 0

       

(3, 0)      (1, 0)

3. Punto de corte con el eje OY

(0, 3)

Sucesiones - Progresiones (Video Explicativo)

Dejo un video que encontre en youtube que lo subo al blog, que explica muy bien las sucesiones y  progresiones con ejemplos de la vida cotidiana.

Trabajo Practico Ingles - Ferreyra William

Para ver mas grande (CONTROL +)

 

TRADUCCÍON

  

Ingles



what´s the mateer? You aren´t concentrating. And you´re running the race next week!





 I know. It´s mery. I´m feeling so depressed about her.

Why don´t you ring her?

I´m not in the mood right now...

How about going to the cinema?

No, I don´t feel like it.

Come on! Cheer up! shall we go to my place? Some of my sister´s friends are coming round this afternoon.

Oh, well, if you want to...










Alumnas: DIANA RUIZ DIAZ              ELENA RIQUELME

Límite

¿Qué es un límite?

Es el valor al cual “se aproxima” una función cuando “x” tiende a un valor determinado”.
El límite de una función, es el valor de “y”, que admite un punto en determinado valor “x”.
Para ello analizamos primero que son los límites laterales.
Dada la función (x)= 2x+1 veamos que pasa a medida que “x” tiende (se aproxima) a 1 vamos a usa para ello la siguiente tabla

Para calcular el límite de la función para “x” tendiendo a 1 tengo que acercarme a 1 por la izquierda y por el derecho.
Así vamos a tener dos límites:

 El límite para “x tendiendo a 1 por la izquierda”
 El límite para “x tendiendo a 1 por la derecha”

Para que exista el límite de una función en un punto, los límites deben ser iguales. Como en el ejemplo que vimos, los limites laterales coinciden, existe el límite de la función para “x” tendiendo a 1 y es igual a 3.

Para calcular el límite
Para calcular un límite hay que reemplazar la “x” por el valor al que quiero que “se acerque o aproxime” o sea el valor al cual tiende “x”.

Ejemplo:

Espero que les agrade el trabajo....Gracias


Fuente:
google
ediciones logicamente
otros

FUNCION

Llamamos función al término matemático usado para indicar la relación o correspondencia entre dos o más cantidades(por ejemplo, cantidades de X y cantidades de Y) . Se llama función porque para un numero X, “Y” cambia de valor en “función” del que se le da a X.

Cuando las relaciones tienen una característica especial, como leyes que a cada elemento del primer conjunto le corresponde un único elemento del segundo conjunto.

NO SE CUMPLE LA FUNCION, PORQUE UN ELEMENTO DEL PRIMER CONJUNTO ESTA RELACIONADO CON DOS ELEMENTOS DEL SEGUNDO CONJUNTO. EJEMPLO:

TAMPOCO SE CUMPLE CON LA FUNCION SI TRAZO UNA LINEA Y ESTA CORTA MAS DE UNA VES LA CURBA. EJEMPLO:

SI SE CUMPLE LA FUNCION PORQUE LA LINEA CORTA SOLAMENTE UNA VES LA CURBA. EJEMPLO:

Valor absoluto

El valor absoluto o módulo de un número, constituye la distancia de un punto a al origen. En la recta que se muestra a continuación la distancia del 3 al origen (0) es 3. De igual forma la distancia del punto -3 al origen (0) también es 3. Esto se apuntaría de la siguiente forma:

│-3│=3

Las barras son leídas como el valor absoluto de lo que está dentro. Sin importar en cual de los lados de la recta real se representa el número. Metódicamente podemos ver que si a es positivo, o sea si se encuentra a la derecha de cero, entonces,

│a│=a

Mientras que si se encuentra a la izquierda del origen, es decir si a es negativo, tenemos que,

│a│=-a

Lo escribimos de este modo,

El valor absoluto de un número real x, es definido como:

Veamos algunos ejemplos

Podemos observar como el valor absoluto a una cantidad positiva permanece igual mientras que a una cantidad negativa le cambia el signo.

La expresión a la cual le estamos tomando valor absoluto es de signo positivo por lo cual el valor absoluto queda igual. Aquí se utilizó la primera parte de la definición.

Si la expresión a la cual le estamos hallando valor absoluto es de signo negativo, el valor absoluto cambiará el signo. Aquí se utiliza la segunda parte de la definición.

Ecuaciones con valor absoluto

Si x es una incógnita en la expresión, entonces no se sabe si x-3 es positivo o negativo. Pero si tenemos la ecuación:

│x-3│=5

Debemos tomar en cuenta las dos posibilidades que tenemos de signo, por lo cual hay dos opciones,

1) x-3=5

2) x-3=-5

La primera opción se da en el caso en que x-3 sea positivo, la segunda opción se da en caso que sea negativo.

Si resolvemos la ecuación tenemos que:

1) x=8

2) x=-2

Consecuentemente estos valores de x satisfacen la ecuación:

│x-3│=5

Las propiedades fundamentales del valor absoluto son:

a) No negatividad

b) Definición positiva

c) Propiedad multiplicativa

d) Propiedad aditiva

Valor absoluto de un número complejo

Un número complejo corresponde a la suma de un número real y un número imaginario. No representan un conjunto que se conforma por una relación binaria de orden parcial en el sentido de los números reales, por lo cual se puede decir que los números complejos no conforman un conjunto ordenado. Se utiliza para este caso una nueva identidad que proporcione entonces otra opción para la definición de valor absoluto si hablamos de complejos. Entonces:

para cualquier número complejo de la siguiente forma,

con x e y como números reales, el valor absoluto de z se define de esta manera:

AHORA VAMOS HACER UN EJERCICIO Y GRAFICARLO:

se crea una tabla de valores, se resuelve y se unen los puntos, ahi queda formado el ejercicio del valor absoluto, que parte desde su ordenada al origen que es = 1

Signo

La función signo es una función definida a trozos o función por partes, la cual es representada habitualmente por medio de sgn(x). Se requiere de varias fórmulas para poder definirlas, cada una de las cuales establece el comportamiento de la función en un cierto fragmento o trozo. La definición cambia según el valor de la variable independiente y esta no depende de ningún factor para cambiar. Una función real f (definida a trozos) de una variable real x es correspondiente a una relación cuya definición es concebida por varios conjuntos disjuntos de su dominio los cuales se denominan sub dominios.

Una función es diferenciable a trozos si cada trozo es diferenciable a lo largo de todo el dominio.

Entonces podemos definir la función signo de las siguientes formas, veamos:

1. Si su conjunto de definición, conjunto de partida o dominio de definición es R y su conjunto imagen {-1;0;1}, o sea:

2. A manera de derivada de la función valor absoluto. Su dominio de definición es R – {0} y su conjunto imagen Im={-1;1}




La derivada constituye cómo una función cambia (valor de la variable dependiente) a medida que su entrada también cambia.
3. sgn(x) = 2u(x) – 1 donde u es la función escalón unitario o Heaviside Step (denominada así en honor al matemático ingles Oliver Heaviside) que se define de la siguiente forma:

Propiedades de la función signo

• La función signo es una función impar, o sea

Podemos clasificar a las funciones según su paridad. Las funciones pueden ser pares, impares o no tener paridad. Esto se debe a la paridad de las potencias de las funciones de potencia que integran cada condición:

La función x elevada a n

a- es una función par si n es un entero par,

b- es una función impar si n es un entero impar.

• Todo número real x puede expresarse como producto de su módulo o valor absoluto y la función signo evaluada en x.

El valor absoluto de un número real es su valor numérico sin tener en cuenta su signo.
• La función signo corresponde a la derivada de la función valor absoluto, (con independencia en cero).




• Es derivable con derivada 0 para todo su dominio con excepción de 0.Pero No es derivable en 0 en el sentido común de derivada.
La función Delta de Dirac es una función generalizada o distribución, fue descubierta y utilizada por primera vez por el físico teórico británico Pail Dirac. Esta función es importante en la teoría de las distribuciones (también se conoce como función generalizada) ya que la derivada de la función signo puede ser dos veces la función delta de Dirac.

Funcíon Racional

Una función racional es un cociente entre 2 valores donde el divisor al que llamaremos Q(x) debe ser diferente de 0.
Dibujaré un grafico para así dejar claro el concepto:

Función irracional

Es aquella que incluye a una raíz, que puede ser en cualquier orden o un exponente fraccionario.

Dibujaré un grafico para así dejar claro el concepto:

Funcion Cuadratica

Función cuadrática

En matemáticas una función cuadrática o función de segundo grado es una función polinómica que se define mediante un polinomio de segundo grado como:

Gráficas de funciones cuadráticas.

donde a, b y c son constantes y a es distinto de 0.

La representación gráfica en el plano XY haciendo:

esto es:

es una parábola vertical, orientada hacia arriba o hacia abajo según el signo de a.

Estudio de la función

Corte con el eje y

La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):

lo que resulta:

la función corta el eje y en el punto (0, c), siendo c el termino independiente de la función.

Corte con el eje x

La función corta al eje x cuando y vale 0, dada la función:

tendremos que:

las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen como es sabido por la expresión:

donde:

se le llama discriminante, Δ:

según el signo del discriminante podemos distinguir:

Discriminante positivo

Δ > 0, la ecuación tiene dos soluciones, y por tanto la parábola cortara al eje x en dos puntos: x₁ y x₂.

Veamos por ejemplo la función: walter

que cortara el eje x cuando:

que tendrá por solución general:

en este caso:

que resulta:

Para esta ecuación el discriminante tiene valor positivo:

y por tanto tiene dos soluciones:

operando:

Los puntos: (-1,0), (5,0) son los de corte con el eje x, como se puede ver en la figura.

Discriminante nulo

 

Δ = 0, la ecuación tiene una única solución en x₁, la parábola solo tiene un punto en común con el eje x, el cual es el vértice de la función donde las dos ramas de la parábola confluyen.

si la función cuadrática:

que cortara al eje de las x si:

su solución sera:

Operando los valores, tendremos:

la raíz de cero es cero, luego el discriminante en este caso vale cero, y habrá una única solución:

El punto de corte de la función con el eje de las x es (2,0), que en este caso es tangencial de la función con el eje, ver figura.

Discriminante negativo

Δ < 0, la ecuación no tiene solución real, y la parábola no corta al eje x.

Si tenemos la función siguiente:

que corta el eje x cuando:

para encontrar su solución haremos:

Haciendo las operaciones, tendremos:

Al no existir ningún número real que sea la raíz de –8, no se puede continuar haciendo las operaciones, por lo que podemos decir que esta función no tiene corte con el eje x, como se ve en la figura.

Si tenemos en cuenta la existencia de los números imaginarios, podemos realizar las siguientes operaciones:

Continuando con las operaciones:

dando como solución:

Dado el plano cartesiano xy, real, la parábola vista no corta el eje real x en ningún punto, esa misma ecuación estudiada dentro de los números complejos presenta dos soluciones, cumpliéndose de este modo el Teorema fundamental del álgebra.

Extremos relativos

Para localizar los extremos relativos, se calcula la derivada de la función, y se iguala a cero, la solución a esta ecuación son los posibles máximos y mínimos de la función, en este caso, partiendo de la función cuadrática:

calculamos su derivada respecto a x:

que si la igualamos a cero, tenemos:

donde x valdrá:

En la vertical que pasa por este valor de x se encontrar el valor máximo o mínimo relativo de la función.

Para saber si es un máximo o un mínimo es necesario ver la derivada segunda de la función, veamos:

esto es: 2a será positivo cuando a sea positivo y negativo si a es negativo, por tanto, si la derivada segunda 2a es positiva la parábola es cóncava y el punto será un mínimo de la función, si a es negativa la parábola será convexa y sea un máximo.

Ejemplo 1

Dada la función:

De la figura, calcularemos su derivada primera:

Esta derivada valdrá cero:

cuando:

esto es:

Esta función presenta un extremo relativo para

  

veamos si es un máximo o un mínimo, calculando la derivada segunda:

Que es 2, dado que 2 es un valor positivo, la función es concava, y el extremo relativo que presente para :

es un mínimo. El valor de la derivada segunda de una función de segundo grado es el coeficiente de y = x², por lo que a la vista de la ecuación, podíamos adelantar que seria mínimo sin calcular la derivada segunda.

Ejemplo 2

Dada la función:

Para calcular sus extremos relativos calcularemos su derivada primera:

Esta derivada valdrá cero cuando:

esto es:

que resulta:

Para x = 2, la función presenta un extremo relativo, como sabemos que el coeficiente de x², es negativo es un máximo. Si realizamos el estudio de signo de la derivada primera, nos da que en x = 2 pasa de ser positivo a negativo, o sea la función cambia de ser creciente a decreciente, por lo que confirmamos que es un máximo. De otra forma; se puede calcular la derivada segunda en este punto, comprobando si la función es cóncava o convexa.

Forma factorizada

Toda función cuadrática se puede factorizar en función de sus raíces. Dada:

se puede factorizar como:

siendo a el coeficiente principal de la función, por ello se extrae siempre como factor común, de no escribirse, el coeficiente de x² sería siempre 1. x₁ y x₂ representan las raíces de f(x). En el caso de que el Discriminante Δ sea igual a 0 entonces x₁ = x₂ por lo que podríamos escribir:

En este caso a x₁ se la denomina raíz doble, ya que su orden de multiplicidad es 2.

Forma canónica

Toda función cuadrática puede ser expresada mediante el cuadrado de un binomio de la siguiente manera:

A esta forma de expresión se la llama forma canónica. Siendo a el coeficiente principal y el par ordenado (h; k) las coordenadas del vértice de la parábola. Para llegar a esta expresión se parte de la forma polinómica y se realiza el siguiente procedimiento:

• Dado:

• Se extrae a como factor común en el término cuadrático y en el lineal.

• Se completa el trinomio cuadrado perfecto, sumando y restando para no alterar la igualdad.

• Se factoriza formando el cuadrado de un binomio.

• sustituyendo:

• la expresión queda:

Determinar la ecuación conocidos tres puntos.

Partiendo de la forma de la ecuación:

y conocidos tres puntos del plano xy por los que pasa una función polinomica de segundo grado:

se cumplirá que:

con lo que tenemos un sistema de tres ecuaciones con tres incógnitas, donde las incógnitas son: a, b y c, este sistema tendrá solución si el determinante de los coeficientes de las incógnitas es distinto de cero.